The Wang 2200 BASIC used a BCD floating point number system. All numbers are double precision and occupy eight bytes of memory. Internally, the format is: Signs nibble, Exp. Low nibble, Exp. High nibble, Mantissa (13 nibbles). Both the mantissa and exponent are represented as BCD sign/magnitude form.
| Signs | Low Exp. | High Exp. | MS Mantissa digit | ... | LS Mantissa digit |
|---|---|---|---|---|---|
| 1 nibble | 1 nibble | 1 nibble | 1 nibble | 11 more nibbles | 1 nibble |
The mantissa is always normalized. If the exponent gets too small, the value simply flushes to zero (which is encoded as all zero bytes).
The signs nibble has four bits. The ms bit of the sign nibble is 1 if the exponent is negative. The ls bit of the sign nibble is 1 if the mantissa is negative. The other two bits are always zero, or in a Verilog-ish syntax, { exponent_sign, 0, 0, mantissa_sign }. Stated another way, there are four legal values for this sign nibble:
| Sign nibble value | indicates | Example value |
|---|---|---|
| 0 | mantissa and exponent both positive | +1.0 |
| 8 | mantissa positive, exponent negative | +0.1 |
| 9 | mantissa and exponent both negative | -0.1 |
| 1 | mantissa negative, exponent positive | -1.0 |
Wang BASIC-2, which ran on the 2200VP and related CPU, is also BCD and also occupied eight bytes. It is very likely similar if not identical, but it hasn't yet been researched.
Google books turned up an interesting reference in the book Mothers and daughters of invention: notes for a revised history of technology, by Autumn Stanley. Page 482 says that the 2200 microcode for floating point operation was written by Jenny Chuang.
The microcode for the floating routines in BASIC-2 was written by Dave Angel (verified by personal email).
(M)VP Random Number Generator (link)
Calling RND(0) sets the random number seed to a fixed value and returns 0.1584625767084. Every call of RND(1) (really, any non-zero argument) it returns the next pseudo-random number in the sequence, exclusively between 0.0 and 1.0.
The algorithm for generating the sequences was written down by Dave Angel, one of the primary developers of BASIC-2. There are a few parts to the algorithm.
- A 32-bit random number generator seed is maintained
- RND(0) initializes the 32-bit seed to 0x10DF5D09
- Each time a random decimal digit is needed, the 32-bit seed is updated
via this C-like pseudocode. One digit is extracted and returned:
unsigned int seed; // 32b int unsigned int next_digit(bool odd) { unsigned int digit; while (1) { seed = (5*seed) + (seed << 16); digit = (odd) ? ((seed >> 24) & 0xF) // bits [27:24] : ((seed >> 28) & 0xF); // bits [31:28] if (digit < 10) { return digit; } } } - The odd digits of the 13 digit mantissa are filled from msb to lsb via bits [27:24] of the next_digit(true) function
- The even digits of the 13 digit mantissa are filled from msb to lsb via bits [31:28] of the next_digit(false) function
- The mantissa is normalized (in case of leading zeros)
- The resulting value is the value of the call to RND(1)
Below is the output of his verification program for the first RND(1) call after RND(0).
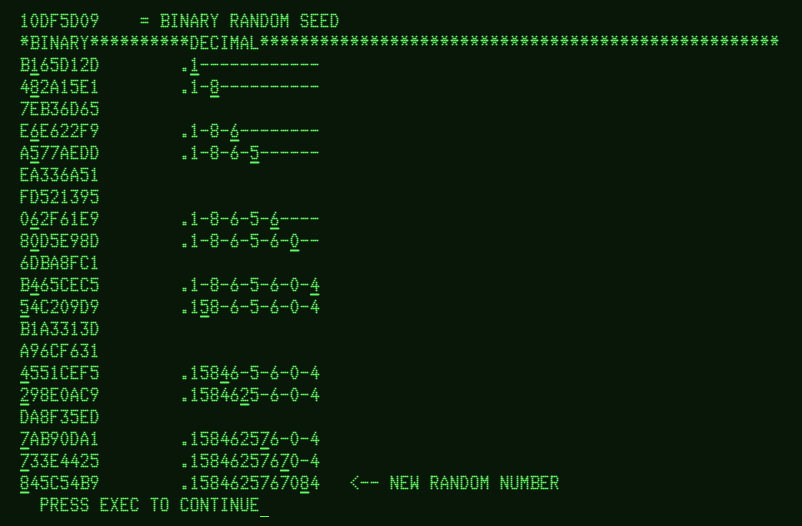
Dave Angel's original memo can be found in the bookmarked section called "Technical Note #2606" in this document.
(M)VP Matrix Inversion Procedure (link)
An internal Wang document, written by Bruce Patterson, who was the lead architect on Wang BASIC and on BASIC-2, describes the algoritm used by BASIC-2 when performing a matrix inversion. The algorithm is outlined, then a version written in BASIC is supplied.
Rather than repeat it here, go to the bookmarked section "Technical Note #2601, BASIC-2 Matrix Inversion" in this document. It is nothing fancy: an in-place Gauss-Jordan algoritm using the maximum pivot strategy.
Wang BASIC Precision Issues (link)
From the same document as before, Roger Droz wrote a very thoughtful article on precision and rouding issues in BASIC and BASIC-2, specifically as it applies to business concerns (the person he was replying to had asked about it in that context).
Roger Droz's article is in the bookmarked section titled "2200 Math Package Precision" in this document.
CPU Microarchitecture Synergy (link)
The 2200 CPU had a few features to make working with floating point BCD numbers more efficient.
- the CPU had instructions for BCD addition and subtraction
- the CPU was a nibble addressed machine with 4b operations
- some addressing modes caused the address pointer to increment or decrement with a wrap at 16 nibbles
- although the CPU was a 4b machine for the most part, reads fetched 8b at a time. There were two modes of reading. In one mode, the 8b were the adjacent nibbles of a byte (horizontal mode). In the other mode, they were corresponding nibbles that were 16 nibbles apart (vertical mode).
Synergy occurs when these separate features work together to mutually enhance the usefulness of each individual feature. In the case of Wang BASIC, the interpreter would place the two operands of whatever operation was being performed (addition, multiplication, etc.) into memory aligned to a 16 nibble boundary with the two operands 16 nibbles apart. By using the vertical read mode, corresponding nibbles of the two operands could be fetched in one memory access. By using autoincrementing addressing, each ALU operation would have the side effect of advancing to the next nibble in the operands. By using the wrapping feature the CPU could sometimes avoid having to reset the nibble pointer at the end of the mantissa operation.
Exploration (link)
Wang BASIC has a few functions for converting between numeric and alphanumeric representations (ASCII or packed hex). Attempts to feed the string to number conversion command malformed strings to see what kind of number is generate has met with no interesting results. For example:
10 A$=HEX(0000000000000000) 20 CONVERT (+#.############^^^^) A$ TO A 30 PRINT A
Produces 0 (mantissa and exponent signs are positive, all mantissa nibbles are zero, exponent is zero). First, some vanilla values; to make it easier to decode, the nibble with the S over it is the signs nibble, the M nibbles are the mantissa digits, and EE are the exponent digits.
SMMMMMMMMMMMMMEE
10 A$=HEX(0000000000000000) --> 0
10 A$=HEX(0100000000000000) --> 1
10 A$=HEX(0150000000000000) --> 1.5
10 A$=HEX(0100000000000001) --> 10 (exponent of positive 01)
10 A$=HEX(8100000000000001) --> 0.1 (exponent of negative 01)
10 A$=HEX(1100000000000000) --> -1 (negative mantissa sign bit)
Now throw in some values that stretch the rules:
SMMMMMMMMMMMMMEE
10 A$=HEX(0010000000000001) --> 1 (unnormalized mantissa is accepted)
10 A$=HEX(8010000000000099) --> error (would be 1E-100; not flushed to zero)
10 A$=HEX(010000000000000A) --> error (illegal exponent nibble value)
10 A$=HEX(2100000000000001) --> 10 (unspecified sign bit is ignored)
10 A$=HEX(4100000000000001) --> 10 (unspecified sign bit is ignored)
The two middle bits of the signs nibble appear to be completely ignored.
